Question

In a cartons of bulbs, 90% contain no defective bulbs, 5% contain one defective bulb, 3% contain two defective bulbs, and 2% contain three defective bulbs. Find the mean and standard deviation for the number of defective bulbs.

Answer 1

Mean, E(x) = 0.17

Variance, V(x) = 0.12

Explanation:

90% contains no defective bulbs, P(X=0) = 0.9

5% contain one defective bulbs, P(X=1) = 0.05

3% contain two defective bulbs, P(X=2) = 0.03

2% contain three defective bulbs, P(X=3) = 0.02

The mean for the number of defective bulbs:

`E(X) = \sum XP(X)\\E(X) = (0*0.9) + (1*0.05) + (2*0.03) + (3* 0.02)\\E(X) = 0 + 0.05 + 0.06 + 0.06\\E(X) = 0.17`

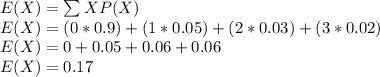
Variance for the defective bulbs:

`V(x) = (\sum x^(2)P(x) ) - \mu^2`

`\sum x^(2)P(x) = (0^2*0.9) + (1^2*0.05) + (2^2*0.03) + (3^2* 0.02)\\\sum x^(2)P(x) = 0.05 + 0.12 + 0.12\\\sum x^(2)P(x) = 0.29`

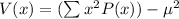
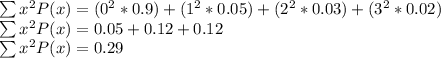
V(x) = 0.29 - 0.17

V(x) = 0.12