1. The volume under the surface
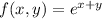 is given by the double integral,
is given by the double integral,
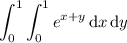
We split up the integration region into a 2x3 grid of rectangles whose upper right corners are determined by the right endpoints of the partition along either axis. That is, we split up the
 interval [0, 1] into 2 subintervals,
interval [0, 1] into 2 subintervals,
[0, 1/2], [1/2, 1]
with right endpoints given by the arithmetic sequence,

for
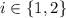 , and the
, and the
 interval [0, 1] into 3 subintervals,
interval [0, 1] into 3 subintervals,
[0, 1/3], [1/3, 2/3], [2/3, 1]
with right endpoints
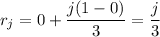
for
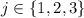 .
.
Then the upper right corners of the 6 rectangles are the points
(1/2, 1/3), (1/2, 2/3), (1/2, 1), (1, 1/3), (1, 2/3), (1, 1)
generated by the sequence
 .
.
The integral is thus approximated by the sum
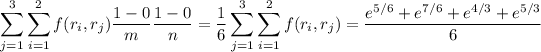
or approximately 2.4334. (Compare to the actual value of the integral, which is close to 2.952.)
For the midpoint rule estimate, we replace the sampling points
 with
with
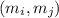 , i.e. the midpoints of each subinterval, so the set of sampling points is
, i.e. the midpoints of each subinterval, so the set of sampling points is
(1/4, 1/6), (3/4, 1/6), (1/4, 1/2), (3/4, 1/2), (1/4, 5/6), (3/4, 5/6)
and the integral is approximately
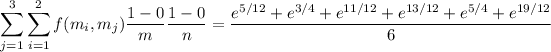
or about 2.908.
2. We approach the second integral the same way. Split up the
 interval into 8 subintervals with left and right endpoints given respectively by
interval into 8 subintervals with left and right endpoints given respectively by
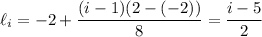
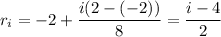
for
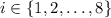 , and the
, and the
 interval into 2 subintervals with
interval into 2 subintervals with
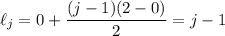
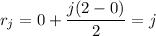
for
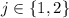 .
.
The upper left corners of the rectangles in this grid are given by the sequence
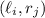 . So the integral is approximately
. So the integral is approximately
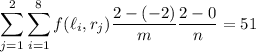
(Compare to the actual value, 32.)