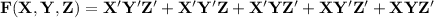Question

Given the function F (X, Y , Z)=Σm(0,1, 2 , 4 , 6)

answer the following questions:

1. Obtain the expression in the Canonical Disjunctive Normal Form

Answer 1

`\mathbf{F(X,Y,Z) = X'Y'Z'+X'Y'Z+ X'YZ'+ XY'Z'+ XYZ'}`

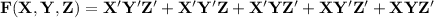
Step-by-step explanation:

Given the function F (X, Y , Z)=Σm(0,1, 2 , 4 , 6)

Σm(0,1, 2 , 4 , 6) = Min. terms and ;

πM = (3, 5, 7 ) = Max. terms

Canonical Disjunctive Normal Form is a SOP term whereby each min. term contains every single variable.

`\mathbf{0 \to X'Y'Z'} \\ \\ \mathbf{1 \to X'Y'Z} \\ \\ \mathbf{2 \to X'YZ'} \\ \\ \mathbf{4 \to XY'Z'} \\ \\ \mathbf{6 \to XYZ'}`

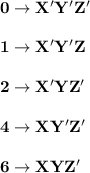
Thus;

`\mathbf{F(X,Y,Z) = X'Y'Z'+X'Y'Z+ X'YZ'+ XY'Z'+ XYZ'}`