Question

What is the simplified form of 1 over x minus 2 over x squared minus x ? (1 point) Question 5 options: 1) x minus 1 over the quantity x times x plus 1 2) 1 minus x over the quantity x times x plus 1 3) 3 minus x over the quantity x times x minus 1 4) x minus 3 over the quantity x times x minus 1

Answer 1

4) x minus 3 over the quantity x times x minus 1

Explanation:

The sum of rational expressions is found the same way the sum of numerical fractions is found. Each part of the sum must be expressed using a common denominator. Then the numerators can be added.

Common denominator

We want to simplify ...

`(1)/(x)-(2)/(x^2-x)`

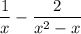
For the purpose of finding a common denominator, it is useful to have each denominator in factored form:

`(1)/(x)-(2)/(x(x-1))`

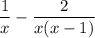
This lets us see that the product of unique denominator factors is x(x-1), so that will be the common denominator we want to use.

`=(1)/(x)\cdot(x-1)/(x-1)-(2)/(x(x-1))=((x-1)-2)/(x(x-1))`

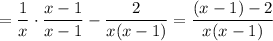
Simplified

The expression is simplified by simplifying the numerator and cancelling any common factors from numerator and denominator. We find there are no common factors, so the simplified form is ...

`=\boxed{(x-3)/(x(x-1))}`