Answer: 307.7 grams
Explanation:
The exponential decay equation with initial value 'A' and rate of decay 'r' ( in decimal) in 't' years is given by :-

As per given , we have
Initial mass of isotope = 1500 grams
Rate of decay : r= 8% =0.08
To find : the mass of the radioactive sample at the beginning of the 20th day of the experiment ( i.e. after 19 days).
That would be ,
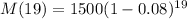 [Using (i)]
[Using (i)]
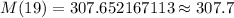 [Rounded to the nearest tenth]
[Rounded to the nearest tenth]
Hence, the mass of the radioactive sample at the beginning of the 20th day of the experiment = 307.7 grams