Answer:
The tree house is 23.09 meters high
Explanation:
Kirsten is sitting in a tree house reading and notices her dog Penny starting to dig a hole 40 meters away from the base of the
tree. Penny, the dog, looks up at Kirsten in the tree house at an angle of elevation of 30°, then continues to dig. How high is the
tree house?
To find the height of the tree house, we will follow the steps below;
we can use the trigonometric ratios to solve the problem
SOH CAH TOA
sin Ф = opposite / hypotenuse
cosФ = adjacent / hypotenuse
tan Ф = opposite / adjacent
From the diagram below,
angle Ф = 30°
adjacent = 40 meters
opposite = h where h is the height of the tree house
From the parameters we have, the best trigonometric ratio to use is tan
tan Ф = opposite / adjacent
tan 30° =
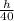
cross-multiply
h = 40 tan 30°
h ≈ 23.09 meters
Therefore, the tree house is 23.09 meters high