Answer:
907,200 different 10-letter arrangements can be formed using the letters in the word ANTEBELLUM
Explanation:
Number of arrangments:
A word has n letters.
There are m repeating letters, each of them repeating times
So the number of distincts ways the letters can be permutated is:
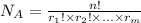
In this question:
ANTEBELLUM has 10 letters.
E and L each occur two times. So
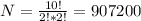
907,200 different 10-letter arrangements can be formed using the letters in the word ANTEBELLUM