Question

Solve the one in the middle asking for f'(10)​

Answer 1

From the definition, we have

`\displaystyle f'(10) = \lim_(x\to0) (f(x) - f(10))/(x - 10)`

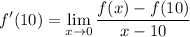
With
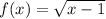`f(x)=√(x-1)`, we get
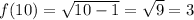`f(10)=√(10-1)=\sqrt9=3`. So the limit we want to compute is

`\displaystyle f'(10) = \lim_(x\to0) (√(x-1) - 3)/(x - 10)`

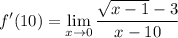
Rationalize the numerator by multiplying by its conjugate:

`\displaystyle (√(x-1) - 3)/(x - 10) * (√(x-1)+3)/(√(x-1)+3) = (\left(√(x-1)\right)^2-3^2)/((x-10)\left(√(x-1)+3\right)) = (x-10)/((x-10)\left(√(x-1)+3\right))`

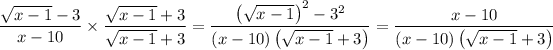
x is approaching 10, which is to say x ≠ 10, so we can cancel the factors of x - 10 and remove the discontinuity.

Then we're left with

`\displaystyle f'(10) = \lim_(x\to0) \frac1{√(x-1)+3} = \frac1{√(10-1)+3} = \frac1{\sqrt9+3} = \frac1{3+3} = \boxed{\frac16}`

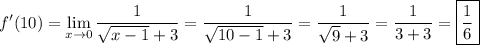
evaluated by direct substitution, which we can do since the limand is continuous.