Question

3. The Human Resources department of a large corporation wants to estimate the mean number

of unused vacation days that its employees have. They conduct a random sample of 30
employees and find a sample mean of 13.6 days. Assuming a standard deviation of 1.4 days,
find the 90% confidence level margin of error for this sample mean. Use z = 1.645. Round
your answer to the one-hundredths place.

*04.08
*1.11
*00.42
*0.08​

Answer 1

The 90% confidence level margin of error for this sample mean is 0.42

Explanation:

The Human Resources department conduct a random sample of 30 employees

n = 30

Standard deviation =
`\sigma = 1.4`

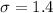
z = 1.645

Formula of 90% confidence level margin of error for this sample mean=
`Z * (\sigma)/(√(n))`

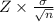
So, margin of error for this sample mean=
`1.645 * (1.4)/(√(30))`

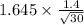
So, margin of error for this sample mean=0.42

Hence the 90% confidence level margin of error for this sample mean is 0.42