Question

Which is the graph of a quadratic equation that has a negative discriminant?

Answer 1

GRAPH D

Explanation:

ENG 2021(:

Answer 2

Here's what I get

Explanation:

The formula for a quadratic equation is

ax² + bx + c = 0

The quadratic formula gives the roots:

`x = (-b\pm√(b^2-4ac))/(2a) = (-b\pm√(D))/(2a)`

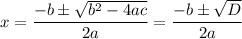
D is the discriminant.

It tells us the number of roots to the equation — the number of times the graph crosses the x-axis.

`D = \begin{cases}\text{positive} & \quad \text{2 real solutions}\\\text{zero} & \quad \text{1 real solution}\\\text{negative} & \quad \text{0 real solutions}\\\end{cases}`

It doesn't matter if the graph opens upwards or downwards.

If D > 0, the graph crosses the x-axis at two points.

If D = 0, the graph touches the x-axis at one point.

If D < 0, the graph never reaches the x-axis.

Your graph must look like one of the two graphs on the right in the Figure below.