Answer:
The true statement about Class B is that Class B has a smaller median and the same inter quartile range.
Explanation:
We are given the ages of students enrolled in two math classes at the local community college, Class A and Class B, below;
Class A: 20, 20, 20, 21, 22, 23, 23, 25, 27, 29, 30, 31, 34, 35, 36, 39, 40
Class B: 16, 17, 18, 18, 20, 22, 22, 24, 26, 26, 28, 29, 30, 34, 37, 40, 42
1) Firstly, we will calculate Median for Class A;
For calculating median, first we have to observe that number of observations (n) in our data is even or odd, that is;
- If n is odd, then the formula for calculating median is given by;
Median =
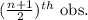
- If n is even, then the formula for calculating median is given by;
Median =
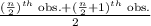
Here, number of observation is odd, i.e. n = 17.
So, Median =
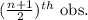
=
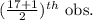
=
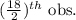
=
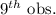 = 27
= 27
Hence, the median of class A is 27.
2) Now, we will calculate Median for Class B;
For calculating median, first we have to observe that number of observations (n) in our data is even or odd, that is;
- If n is odd, then the formula for calculating median is given by;
Median =
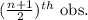
- If n is even, then the formula for calculating median is given by;
Median =
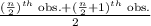
Here, number of observation is odd, i.e. n = 17.
So, Median =
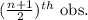
=
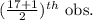
=
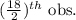
=
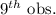 = 26
= 26
Hence, the median of class B is 26.
3) Now, we will calculate the Inter quartile range for Class A;
Inter quartile range = Upper quartile - Lower quartile
=

SO,
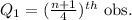
=
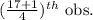
=

=
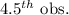
=
![4^(th) \text{ obs.} + 0.5[5^(th) \text{ obs.} - 4^(th) \text{ obs.}]](https://img.qammunity.org/2021/formulas/mathematics/high-school/vdjkdx0j0wiss61xw30w1kj7pxbelace6b.png)
=
![21+ 0.5[22- 21]](https://img.qammunity.org/2021/formulas/mathematics/high-school/t4x64lkareujiv89szkn64z2pnfmiiivhl.png)
= 21.5
Similarly,
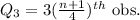
=
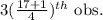
=
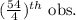
=
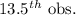
=
![13^(th) \text{ obs.} + 0.5[14^(th) \text{ obs.} - 13^(th) \text{ obs.}]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ymypy8ucqoymdvkzssj48wy932ur7pkh2d.png)
=
![34+ 0.5[35- 34]](https://img.qammunity.org/2021/formulas/mathematics/high-school/v2tciz4d5div93u6se0tz1rljowaw2hxxn.png)
= 34.5
Therefore, Inter quartile range for Class A = 34.5 - 21.5 = 13.
4) Now, we will calculate the Inter quartile range for Class B;
Inter quartile range = Upper quartile - Lower quartile
=

SO,
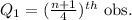
=
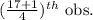
=

=
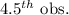
=
![4^(th) \text{ obs.} + 0.5[5^(th) \text{ obs.} - 4^(th) \text{ obs.}]](https://img.qammunity.org/2021/formulas/mathematics/high-school/vdjkdx0j0wiss61xw30w1kj7pxbelace6b.png)
=
![18+ 0.5[20- 18]](https://img.qammunity.org/2021/formulas/mathematics/high-school/rjlxrlg5pbmqj0sd6xfbc7ujpvstam10n0.png)
= 19
Similarly,
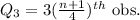
=
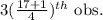
=
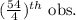
=
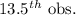
=
![13^(th) \text{ obs.} + 0.5[14^(th) \text{ obs.} - 13^(th) \text{ obs.}]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ymypy8ucqoymdvkzssj48wy932ur7pkh2d.png)
=
![30+ 0.5[34- 30]](https://img.qammunity.org/2021/formulas/mathematics/high-school/j8ow1jmii414e78mpgqckf76zfwu9420om.png)
= 32
Therefore, Inter quartile range for Class B = 32 - 19 = 13.
Hence, the true statement about Class B is that Class B has a smaller median and the same inter quartile range.