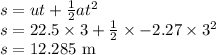Question

A truck travelling at 22.5 m/s decelerates at 2.27 m/s2. (a) How much time does it take for the truck to stop? (b) How far does it travel while stopping? (c) How far does it travel during the third second after the brakes are applied?​

Answer 1

We can use the "suvat" method

s is displacement

u is initial velocity

v is final velocity

a is acceleration

t is time

We substitute in what we know...

s = ?

u = 22.5 (the speed/velocity the trucks is initially)

v = 0 (the truck comes to a stop)

a = -2.27 (negative because it is decelerating

t = ?

`\text{suvat formulae}:\\v = u + at\\s = ut + (1)/(2)at^2\\v^2 = u^2 + 2as\\s = (v+u)/(2)t\\s = vt - (1)/(2)at^2`

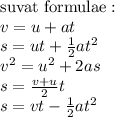
We have
`u`,
`v`,
`a` and we want to find the time for how long it takes the truck to stop.

We can use
`v = u + at`

`v = u + at\\0 = 22.5 - 2.27 * t\\(-22.5)/(-2.27) = t\\t = 9.91...\ \text{s}`

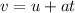
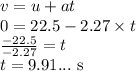
To find the distance (displacement), we can use
`s = ut + (1)/(2)at^2`

`s = ut + (1)/(2)at^2\\s = 22.5 + (1)/(2) * -2.27 * 9.91^2\\s = -88.9661935\ \ \text{(we make it positive since you can't have negative distance)}\\s = 88.97...\ \text{m}`

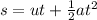
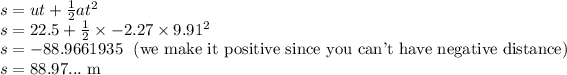
To find the distance travelled 3 seconds after breaks are applied;

We just use the same formula, but with
`t = 3`

`s = ut + (1)/(2)at^2\\s = 22.5 * 3 + (1)/(2) * -2.27 * 3^2\\s = 12.285\ \text{m}`