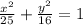Question

4. A horizontal ellipse, centered at the origin has a major axis of 10 units and minor axis of 8 units. Write the

equation of the ellipse.

Answer 1

`(x^2)/(25) +(y^2)/(16) =1`

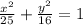
Explanation:

For ellipses, the length of the major axis is represents as:

Major axis =
`2a`

where
`a` is called the semi-major axis.

In this case since the major axis is equal to 10 units:

`10=2a`

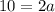
solving for the semi-major axis
`a` :

`a=10/2\\a=5`

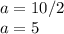
and also the minor axis of an ellipse is represented as:

Minor axis =
`2b`

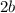
where
`b` is called the semi-minor axis.

Since the minor axis has a length of 8 units:

`8=2b`

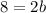
solving for b:

`b=8/2\\b=4`

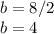
Now we can use the equation for an ellipse centered at the origin (0,0):

`(x^2)/(a^2) +(y^2)/(b^2) =1`

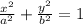
and substituting the values for
`a` and
`b`:

`(x^2)/(5^2) +(y^2)/(4^2) =1`

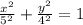
and finall we simplify the expression to get the equation of the ellipse:

`(x^2)/(25) +(y^2)/(16) =1`