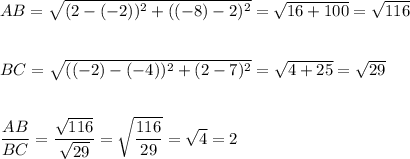Question

Point A is at (2,-8) and the point C is at (-4,7). Find the coordinates of point B on AC such that the ratio of AB to BC is 2:1.

Answer 1

Answer: (-2,2)

Explanation:

Answer 2

The coordinates of point B are (-2, 2)

Explanation:

We have two points: A and C.

The coordinates for A are (2, -8) and the coordinates for C are (-4, 7).

We have to find the coordinates of the point B, that satisfies the condition that the distance AB is 2 times the distance BC.

We also know that B is a point of the line AC.

We can calculate the line AC as a linear function y=mx+b.

The slope m is:

`m=(y_c-y_a)/(x_c-x_a)=(7-(-8))/(-4-2)=(15)/(-6)=-2.5`

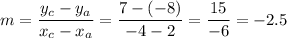
Then, the y-intercept b can be calculated using the coordinates of one of the points, in this case point A:

`y=-2.5x+b\\\\b=y_a+2.5x_a=-8+2.5*2=-8+5=-3`

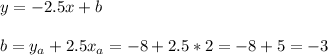
Then, we know that B is a point of the linear function y=-2.5x-3, within the range x ∈ (-4; 2).

To have a ratio AB to BC of 2 to 1, we can divide the length of the line AC in 3 parts, and the point B will be located in the end of the segment nearer to point C.

In the picture attached, you can see the division of the segment AC in three parts and the location of point B=(x, y).

Applying the Thales theorem, we can divide the segment in the y-axis in three and calculate y, and the same for the x-axis.

Then, the coordinate y for the point B is:

`y=y_c-(y_c-y_a)/3\\\\y=7-[7-(-8)]/3=7-15/3=7-5=2\\\\\\x=x_c-(x_c-x_a)/3\\\\x=-4-(-4-2)/3=-4-(-6)/3=-4+2=-2`

Then, the point B has coordinates (-2, 2).

We can verify the distances as:

`AB=√((2-(-2))^2+((-8)-2)^2)=√(16+100)=√(116)\\\\\\BC=√(((-2)-(-4))^2+(2-7)^2)=√(4+25)=√(29)\\\\\\(AB)/(BC)=(√(116))/(√(29))=\sqrt{(116)/(29)}=√(4)=2`