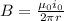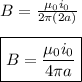Question

The figure shows the cross section of a long cylindrical wire of

radius aa, which carries a uniform current ii0. Determine the module of the field

magnetic produced by the current at a distance from the axis of the wire equal to (a)

0, (b) a/2, (c) a (wire surface) and (d) 2a.

Answer 1

Hi there!

Recall Ampere's Law:

`\oint B \cdot dl = \mu_0 i_(encl)`

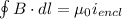
B = Magnetic Field Strength (T)
μ₀ = Permeability of Free Space (Tm/A)

i = Enclosed Current (A)

dL = differential path length

To begin, we must derive an expression for the magnetic field strength inside a wire that contains a uniformly-distributed current.

Using the expression:

`i = \int J \cdot dA`

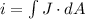
Where 'J' is the density of current, and A is the cross-sectional area:

`A = \pi r^2\\\\dA = 2\pi r dr`

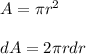
We know that:

`J = (i_0 )/(A)\\\\J = (i_0)/(\pi a^2)`

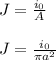
This is the current density. We can now integrate:

`i = \int\limits^r_0 {(i_0)/(\pi a^2) \cdot 2\pi r} \, dr\\ \\i =(i_0)/(a^2)\int\limits^r_0 {2r } \, dr\\\\i = (i_0)/(a^2) \cdot r^2 = (i_0 r^2)/(a^2)`

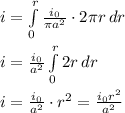
Now, substitute this expression back into the above equation for the magnetic field:

`\oint B \cdot dl = \mu _0 (i_0r^2)/(a^2)`

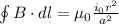
The path of integration is a closed loop of length 2πr, so:

`B \cdot 2\pi r = \mu_0 (i_0r^2)/(a^2)\\\\B = (\mu_0 i_0r)/(2\pi a^2)`

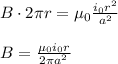
We can now use this equation for the first 2 parts.

a)
If 'r' equals 0:

`B = (\mu _0 i_0 (0))/(2\pi a^2) = \boxed{0 T}`

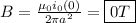
b)

If 'r' equals a/2:

`B = (\mu _0 i_0 ((a)/(2)))/(2\pi a^2) =B =\boxed{ (\mu _0 i_0 )/(4\pi a) T}`

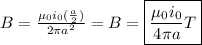
c)
At the wire's surface, 'r' = a:

`B = (\mu _0 i_0 (a))/(2\pi a^2) =B =\boxed{ (\mu _0 i_0 )/(2\pi a) T}`

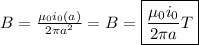
d)

At 'r' = 2a, since this is outside of the wire, the relationship between magnetic field and distance from the wire becomes a 1/r (inverse) relationship. This is found using Ampere's Law:

`B = (\mu_0 i_0)/(2\pi r)\\`

`B = (\mu_0 i_0)/(2\pi (2a)) \\\\\boxed{B = (\mu_0 i_0)/(4\pi a)\\}`