Answer:
203 rpm
Explanation:
The speed of the larger gear can be calculated using the following equation:
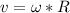
Where:
ω: is the angular velocity of the motor = 700 rpm
R: is the gear ratio
The gear ratio is the following:
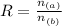
Where:
n(a): is the number of teeth on the small gear = 12 teeth
n(b): is the number of teeth on the larger gear = 42 teeth
The gear ratio is:
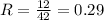
Now, the speed of the larger gear is:
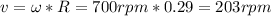
Therefore, the speed of the larger gear is 203 rpm.
I hope it helps you!