Answer:
Therefore, the 95% confidence interval would be given by= (0.0771 , 0.1309)
Explanation:
Given : Sample size=n=500
Let, X be the number of preterm.
Here , X=52
The sample proportion is , p=X/n=52/500=0.1040
q= 1 - p = 0.8960
Therefore , the 95% confidence interval estimate for the percent of preterm of births this year is ,
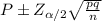
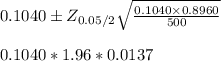
From normal probability integral table;
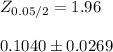
Therefore, the 95% confidence interval would be given by= (0.0771 , 0.1309)