A sphere and a cylinder have the same radius and height. The volume of the cylinder is 18 cm What is the volume of the sphere? O 12 cm O 24 cm O 36 cm 54 cm

Question

asked Jan 10, 2021 208k views

1 Answer

Krish Lakshmanan · Answer 1 · 2021-01-16T02:19:42+0000

We have been given that a sphere and a cylinder have the same radius and height.

We know that height of sphere is equal to its radius. So
h=r .

Now we will use volume of sphere and volume of cylinder formula to solve our given problem.

Volume of cylinder:
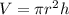$V=\pi r^2h$ , where,

r = Radius,

h = Height

Volume of sphere:
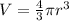$V=(4)/(3)\pi r^3$ , where,

r = Radius.

Since height is equal to radius, so we will get:

$V=\pi r^2\cdot r=\pi r^3$

Since volume of cylinder is
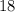cubic cm, so we will equate volume formula with
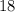as:

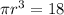
$\pi r^3=18$

Let us solve for r.

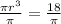
$(\pi r^3)/(\pi)=(18)/(\pi)$

$r^3=(18)/(\pi)$

$r=\sqrt[3]{(18)/(\pi)}$

Upon substituting this value in volume of sphere formula, we will get:

$V=(4)/(3)\pi\cdot \left(\sqrt[3]{(18)/(\pi)}\right)^3$

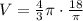
$V=(4)/(3)\pi\cdot (18)/(\pi)$

$V=(4)/(1)\cdot 6$

V=24

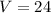
Therefore, the volume of the sphere would be 24 cubic cm and option B is the correct choice.