Question

Verify tan(α+β) = [tan(α)+tan(β)] / [1 + tan(α)tan(β)]

- use the angle sum formula for cosine, the angle sum formula for sine, and the identity tan(x) = sin(x)/cos(x) to verify it.

Answer 1

Proved

Explanation:

To Prove:
`tan(\alpha+\beta) =(tan(\alpha)+tan(\beta))/(1 + tan(\alpha)tan(\beta))`

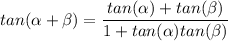
Proof:

Now:
`tan \theta =(sin\theta )/(cos \theta)`

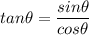
Therefore:

`tan (\alpha+\beta)=( sin (\alpha+\beta))/(cos (\alpha+\beta) )`

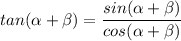
Applying these angle sum formula

`sin (\alpha+\beta)=sin \alpha cos \alpha + sin \beta cos \beta\\cos (\alpha+\beta)=cos \alpha cos \beta - sin \alpha sin \beta`

`tan (\alpha+\beta)=( sin \alpha cos \alpha + sin \beta cos \beta)/(cos \alpha cos \beta - sin \alpha sin \beta )`

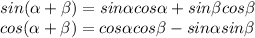
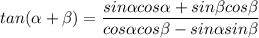
Divide all through by
`cos \alpha cos \beta`

`tan (\alpha+\beta)=( (sin \alpha cos \alpha)/(cos \alpha cos \beta) + (sin \beta cos \beta)/(cos \alpha cos \beta))/((cos \alpha cos \beta)/(cos \alpha cos \beta) - (sin \alpha sin \beta)/(cos \alpha cos \beta) )\\\\tan (\alpha+\beta)=((sin \alpha)/(cos \alpha)+(sin \beta)/(cos \beta) )/(1-tan \alpha tan \beta) \\$Therefore:\\\\tan (\alpha+\beta)=(tan \alpha+tan \beta)/(1-tan \alpha tan \beta)`

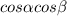
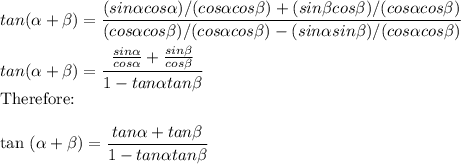
=sin \alpha cos \beta + cos \alpha sin \beta/cos \alpha cos \beta/cos \alpha cos \beta- sin \alpha sin \beta/cos \alpha cos \beta

=sin \alpha/cos \alpha + sin \beta/cos \beta/1-tan \alpha tan \beta

=tan A + tan B/1-tan A tan B