Question

A particular type of cell increases by 75% in number every hour. Find the number of cells present at the end of 12 hours if there are initially 4 of these cells?

Answer 1

We have been given that a particular type of cell increases by 75% in number every hour. We are asked to find the number of cells present at the end of 12 hours if there are initially 4 of these cells.

We will use exponential growth formula to solve our given problem.

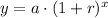`y=a\cdot (1+r)^x`, where,

y = Final amount,

a = Initial amount,

r = Growth rate in decimal form,

x = Time.

`75\%=(75)/(100)=0.75`

Upon substituting initial value
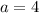`a=4` and
`x=12` in above formula, we will get:

`y=4\cdot (1+0.75)^(12)`

`y=4\cdot (1.75)^(12)`

`y=4\cdot 825.0050068497657776`

`y=3300.020027`

`y\approx 3300`

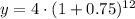
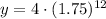
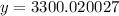
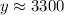
Therefore, there will be approximately 3300 cells at the end of 12 hours.