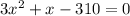Question

The length of a rectangle is 1 more meter than three times its width. The rectangle has an area of 310 m².

Let w represent the width of the rectangle. What quadratic equation, in standard form, represents this situation?

Answer 1

`3x^2 +x -310 = 0`

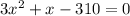
Explanation:

Let the width of rectangle be x m.

Given that length is 1 more than 3 times of times of width

Then width of rectangle in terms of x = 3x+1 (3 time width is 3x then added 1)

Area of rectangle is given by length * width

thus area of the given rectangle in terms of x = x*(3x+1) = 3x^2 +x

also area is given as 310 meter square.

Thus it can be said that

3x^2 +x = 310 subtracting 310 from both sides

=> 3x^2 +x -310 = 310 - 310

=> 3x^2 +x -310 = 0

Thus, quadratic equation, which in standard form, represents this situation is given below

`3x^2 +x -310 = 0`