Question

When Lin drives a golf ball, it travels a mean distance of 200 yards with a standard deviation of 20 yards, and the distribution of lengths is approximately normal. Approximately what percentage of her shots will travel less than 180 yards?

Answer 1

The percentage of her shots that will travel less than 180 yards is approximately 15.9%

Explanation:

First it will be required to find the standard or z-score from the following formula

`z = (x- \mu)/(\sigma)`

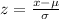
Where:

z = z or standard score

x = value that is observed = 180 yards

μ = Sample mean = 200 yards

σ = Sample standard deviation yards

Plugging the values, we have;

`z = (180- 200)/(20) = -1`

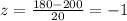
Therefore, the probability that her shots will travel less than 180 is given by the relation;

p( x < 180 yards) = p(z < -1) = 0.15866

Therefore, the percentage of her shots that will travel less than 180 = 0.15866 × 100

= 15.866% ≈ 15.9%.