Question

A forest ranger is on a lookout tower in a forest. His observation tower is 214.7 feet above the

ground when he spots an illegal forest fire. The angle of elevation from the fire to the top of
the lookout is 78 degrees. Find the distance between the base of the tower and the fire. Round
your answer to the nearest tenth (you do not have to include units in you answer)

Answer 1

Let x represent distance between the base of the tower and the fire.

We have been given that a forest forest ranger is on a lookout tower in a forest. His observation tower is 214.7 feet above the ground when he spots an illegal forest fire. The angle of elevation from the fire to the top of the lookout is 78 degrees.

To find the distance between the base of the tower and the fire, we will use trigonometric ratio.

First of all, we will draw a right triangle using our given information as shown in the attached image.

We can see that x is adjacent side and 214.7 is opposite side to angle 78 of degrees.

`\tan=\frac{\text{Opposite}}{\text{Adjacent}}`

`\tan(78^(\circ))=(214.7)/(x)`

`x=(214.7)/(\tan(78^(\circ)))`

`x=(214.7)/(4.704630109478)`

`x=45.63589379`

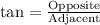
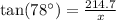
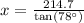
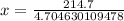
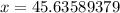
Upon rounding to nearest tenth, we will get:

`x\approx 45.6`

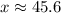
Therefore, the distance between the base of the tower and the fire is approximately 45.6 feet.