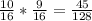Question

A bag contains 10 red beads and 6 white beads. You randomly choose one bead, and then randomly choose another bead. Find the probability that both beads are red if you do not replace the first bead before choosing the second bead.

Answer 1

`(45)/(128)`

Step-by-step explanation:

In order to calculate the probability of this exact sequence you need to find the probability of each separate action and multiply them together. So for the first pick there is a total of 16 beads (10 red + 6 white), 10 of which are red,

so the probability of choosing a red bead in the first pick is
`(10)/(16)`

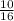
Now since we did not replace the bead then there is now a total of 15 beads left (16 - 1 = 15), and one less red making it 9 red.

so the probability of choosing a red bead in the second pick is
`(9)/(16)`

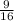
Now we multiply both together to get the probability of the sequence. which is multiplying the numerators together and the denominators together.

`(10)/(16) * (9)/(16) = (45)/(128)`