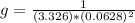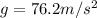Answer:
The value of g is
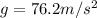
Step-by-step explanation:
From the question we are told that
The mass of the weight is
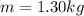
The spring constant
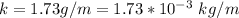
The second harmonic frequency is
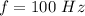
The number of oscillation is
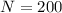
The time taken is
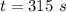
Generally the frequency is mathematically represented as
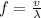
At second harmonic frequency the length of the string vibrating is equal to the wavelength of the wave generated
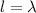
Noe from the question the vibrating string is just half of the length of the main string so
Let assume the length of the main string is
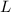
So
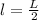
The velocity of the vibrating string is mathematically represented as
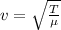
Where T is the tension on the string which can be mathematically represented as
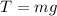
So
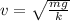
Then
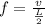
=>
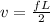
=>
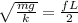
=>
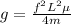
substituting values
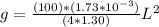
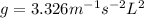
Generally the period of oscillation is mathematically represented as
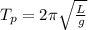
=>
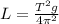
The period can be mathematically evaluated as
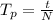
substituting values
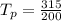
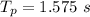
Therefore
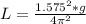
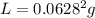
so
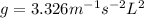
substituting for L
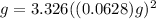
=>