Answer:
Step-by-step explanation:
(a) i. Payment = $7000
For cash flow payment = $750 (Per year at 5%, for 12 years)
= 750*8.863
= $6697.25
This shows it is better to receive $7000 right now.
ii. FV = $10000
PV = FV(P/F, 5%, 10 years)
= 10000*0.6139
= $6139
And Payment of $1000 per year, for 5 years
PV = 1000 (per year at 5%, for 5 years)
= $1000*7.722
= $7722
It is better to get $1000 per year for 5 years
(b)i. PV = $1000
fV = $1402.55
Interest = i
by formula
1000 = 1402.55 (p/f, i, 5)
1000 =
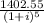
![\sqrt[5]{(1 + i)^5}](https://img.qammunity.org/2021/formulas/business/college/50z0kta4jny62zn74e8s32bqvjixh6jo8c.png) =
=
![\sqrt[5]{(1402.55)/(1000) }](https://img.qammunity.org/2021/formulas/business/college/ic57y7ih20ot0o5eud6tpi9x5tphyqw0e2.png)
1 + i = 1.069
Collect like terms
i = 1.069 - 1
i = 0.069
i ≈ 7%
ii. PV = $166666.67
Perpetuity = 15000
interest is unknown
166666.67 = 15000/i
i = 15000/166666.67
i = 0.089
i ≈ 9%