Question

A ladder is leaning against a house at an angle of 39°. If the latter is 12 feet long, how far is the bottom of the ladder from the house?

Answer 1

The bottom of the ladder is 7.55 feet far away from the house

Explanation:

To find the distance between the bottom of the ladder from a house if a ladder of 12 feet long is leaning against a house at an angle of 39°, then we will follow the steps below:

We can use trig ratios to find the solution to this problem

SOH CAH TOA

sinФ= opposite/hypotenuse

cosФ=adjacent/hypotenuse

tanФ=opposite /adjacent

from the diagram below;

angle Ф=39°

hypotenuse =12 feet

opposite = x where x is the distance of the bottom of the ladder from the house

Given these parameter, the best trig function to use sine

sinФ = opposite / hypotenuse

sin 39° =
`(X)/(12)`

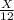
cross-multiply

x = 12 sin 39

x ≈ 7.55 feet

Therefore, the bottom of the ladder is 7.55 feet far away from the house

Answer 2

Answer: 9.32 ft

Explanation:

Hi, since the situation forms a right triangle (see attachment) we have to apply the next trigonometric function.

Cos α = adjacent side / hypotenuse

Where α is the angle of elevation of the ladder to the ground, the hypotenuse is the longest side of the triangle (in this case is the length of the ladder), and the adjacent side (x) is the distance between the bottom of the ladder and the house.

Replacing with the values given:

cos 39 = x/ 12

Solving for x

cos39 (12) =x

x= 9.32 ft

Feel free to ask for more if needed or if you did not understand something.