Answer:
c = 45.33, C =97°, a = 40, A = 61.15° , B = 21.85°, b = 17
Explanation:
Given that:
C = 97°, a = 40 and b = 17.
We have angle C, we need to find the side the side c opposite to the angle C. we have side a, we need to find the angle A opposite to side a. we have side b, we need to find the angle B opposite to side b.
Using cosine rule:
c² = a² + b² - 2ab × cos(C)
c² = 40² + 17² - 2(40)(17)cos(97)
c² = 2054.74
c = 45.33
Also using sine rule:
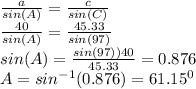
Also:
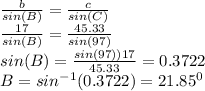
c = 45.33, C =97°, a = 40, A = 61.15° , B = 21.85°, b = 17