Question

Un ladrón viaja en un auto a una velocidad excesiva de 30m/s, en dicho momento un policía de tránsito, lo observa y monta en su moto justo en el momento que pasa por su lado, produciéndose una persecución. Luego de 10 s la moto del policía alcanza una velocidad de 50m/s. Calcular al cabo de qué tiempo, el policía, alcanza al ladrón.

Answer 1

t = 12 s

Step-by-step explanation:

To find the time in which the police reaches the thief you write the equation of motion of both thief and police:

The thief has a constant velocity, the position is then given by:

`x=vt` (1)

The police has an acceleration, then the position is:

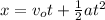`x=v_ot+(1)/(2)at^2` (2)

the time in which the police reaches the thief is when their positions are equal, that is, when expression (1) equals expression (2). But before you calculate the acceleration of the police:

`a=(v-v_o)/(t)\\\\v_o=0m/s\\\\a=(50m/s)/(10s)=5(m)/(s^2)`

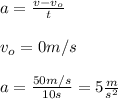
you replace this values in (2) and you equal the expression (1) and (2) (with vo = 0):

`vt=(1)/(2)at^2\\\\(1)/(2)at^2-vt=0\\\\((1)/(2)at-v)t=0`

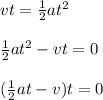
one root is t = 0s, but it is omitted because is the momment in which the thief pass in front of the police. The other root is:

`(1)/(2)at-v=0\\\\t=(2v)/(a)=((2)(30m/s))/(5m/s^2)=12s`

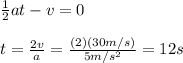
hence, the time is 12 s