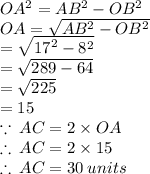Question

For parallelogram ABCD, what is the perimeter and measure of AC?

Answer 1

Perimeter = 68 Units

Answer:

AC = 30 Units

Explanation:

The diagonals AC and BD of parallelogram ABCD are bisecting each other by making 90° angle, this tells us that it is a RHOMBUS.

All sides of rhombus are congruent.

AB = 17 units....(given)

Therefore,

Perimeter = 4*17 = 68 Units

Let diagonals AC and BD intersects at point O.

Therefore, by Pythagoras theorem:

`OA^2 = AB^2 - OB^2 \\ OA= √(AB^2 - OB^2 ) \\ = \sqrt{ {17}^(2) - {8}^(2) } \\ = √(289 - 64) \\ = √(225) \\ = 15 \\ \because \: AC = 2* OA \\ \therefore \: AC = 2* 15 \\ \therefore \: AC = 30 \: units \\`