Question

A company makes wax candles in the shape of a solid sphere. Suppose each candle has a diameter of 15 cm. If

the company has a total of 70,650 cm of wax, how many candles can be made?
Use 3.14 for t, and do not round your answer.

Answer 1

We have been given that a company makes wax candles in the shape of a solid sphere. Each candle has a diameter of 15 cm. We are asked to find the number of candles that company can make from 70,650 cubic cm of wax.

To solve our given problem, we will divide total volume of wax by volume of one candle.

Volume of each candle will be equal to volume of sphere.

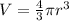`V=(4)/(3)\pi r^3`, where r represents radius of sphere.

We know that radius is half the diameter, so radius of each candle will be
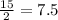`(15)/(2)=7.5` cm.

`\text{Volume of one candle}=(4)/(3)\cdot 3.14\cdot (7.5\text{ cm})^3`

`\text{Volume of one candle}=(4)/(3)\cdot 3.14\cdot 421.875\text{ cm}^3`

`\text{Volume of one candle}=1766.25\text{ cm}^3`

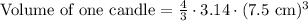
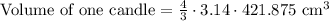
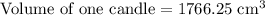
Now we will divide 70,650 cubic cm of wax by volume of one candle.

`\text{Number of candles}=\frac{70,650\text{ cm}^3}{1766.25\text{ cm}^3}`

`\text{Number of candles}=(70,650)/(1766.25)`

`\text{Number of candles}=40`

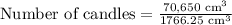
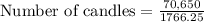
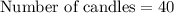
Therefore, 40 candles can be made from 70,650 cubic cm of wax.