Question

One of the most desirable of the old British sports cars was the beautiful Triumph Vitesse (1963-1971). Pictured below is the American version, called the Sports 6. A little expensive back in the day, only 679 were sold. Imagine you are on vacation, and for fun you and your companion select a cool, beautiful day in Gansu Province and ride the G30 highway from Lanzhou to the Mogao caves in Dunhuang, about distance of 686 miles. If you consume gasoline according to:

2 C8H18(l) + 25 O2(g)? 16 CO2(g) + 18 H2O(g)what volume of carbon dioxide gas would be produced by this motoring trip if your fuel consumption was 21.2 miles per gallon? Note that the density of gasoline is 0.805g/cm3, and one mole of any gas at 760 mmHg and 0oC is 22.4 L.

Answer 1

`V_(CO_2)=1.55x10^(5)LCO_2=155m^3CO_2`

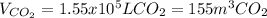
Step-by-step explanation:

Hello,

In this case, given the reaction:

`2 C_8H_(18)(l) + 25 O_2(g)\rightarrow 16 CO_2(g) + 18 H_2O(g)`

The total consumed gallons are computed by considering 686 miles were driven and the consumption is 21.2 miles per gallon, thus:

`V_{C_8H_(18)}=686miles*(1gal)/(21.2miles) =32.4gal`

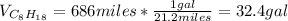
Hence, with the given density, one could compute the consumed grams and consequently moles of gasoline as well as moles that were consumed:

`n_{C_8H_(18)}=32.4gal*(3785.41cm^3)/(1gal) *(0.805g)/(1cm^3) *(1mol)/(114g)=864.95mol C_8H_(18)`

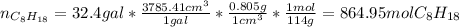
Next, since gasoline (molar mass = 114 is in a 2:16 molar relationship with the yielded carbon dioxide, we compute its produced moles as shown below:

`n_(CO_2)=864.95mol C_8H_(18)*(16molCO_2)/(2molC_8H_(18)) =6919.6molCO_2`

Finally, we could assume the given STP conditions to compute the volume of carbon dioxide, as no more information regarding the space wherein the carbon dioxide is available:

`V_(CO_2)=(n_(CO_2)RT)/(P) =(6919.6mol*0.082(atm*L)/(mol*K)*(0+273)K)/(1atm) \\\\V_(CO_2)=1.55x10^(5)LCO_2=155m^3CO_2`

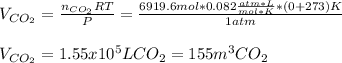
Best regards.