Question

A Pew Internet poll asked cell phone owners about how they used their cell phones. One question asked whether or not during the past 30 days they had used their phone while in a store to call a friend or family member for advice about a purchase they were considering. The poll surveyed 1003 adults living in the United States by telephone. Of these, 462 responded that they had used their cell phone while in a store within the last 30 days to call a friend or family member for advice about a purchase they were considering.

A) Identify the sample size and the count.
B) Calculate the sample proportion.
C) Explain the relationship between the population proportion and the sample proportion.

Answer 1

A) Sample size n=1003

Count x=462

B) Sample proportion p=0.46

C) The population proportion can be estimated with a confidence interval, with the information given by the sample proportion.

The 95% confidence interval for the population proportion is (0.429, 0.491).

Explanation:

A) The sample size include all the adult that answer the poll. The sample size is then n=1003.

The count is the number of adults that answer Yes in this case. The count is x=462.

B) The sample proportion can be calculated dividing the count by the sample size:

`p=(x)/(n)=(462)/(1003)=0.46`

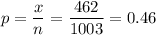
C) The population proportion is not known. It can only be estimated with the information given by samples of that population. The statistical inference is the tool by which the sample information can be used to estimate the population characteristics.

With the sample proportion p we can estimate a confidence interval for the population proportion.

We can calculate a 95% confidence interval.

The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.46*0.54)/(1003)}\\\\\\ \sigma_p=√(0.00025)=0.0157`

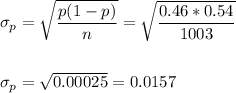
The critical z-value for a 95% confidence interval is z=1.96.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=1.96 \cdot 0.0157=0.031`

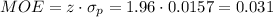
Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.46-0.031=0.429\\\\UL=p+z \cdot \sigma_p = 0.46+0.031=0.491`

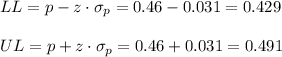
The 95% confidence interval for the population proportion is (0.429, 0.491).

We have 95% that the population proportion is within this interval

Answer 2

Given:

n = 1003

`p' = (462)/(1003) = 0.4606`

q = 1 - 0.4606 = 0.5394

a) The sample size and count.

Here the sample size is the number that took part in the poll. It is denoted as n = 1003.

The count is the number that answered yes. Count = 462

b) The sample proportion.

The formula for sample proportion is:
`p' = (x)/(n)`

Therefore, sample proportion =

`p' = (462)/(1003) = 0.4606`

c) The relationship between population proportion and sample proportion.

Since the sample size is greater than 30 (n>30), the sample size is large. Hence, for a large sample, the population proportion is approximately equal to the sample proportion.

This means the population proportion, p = 0.4606