Question

Y = [ 1 and u = [ 6

3 ] 2 ]
Write y as the sum of a vector in Span {u} and a vector orthogonal to u.
y = z = ___ + ___. ​(Type an integer or simplified fraction for each matrix element. List the terms in the same order as they appear in the original​ list.)

Answer 1

Take
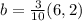`b = (3)/(10)(6,2)` as the vector in Span(u) and
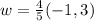`w =  (4)/(5)(-1,3)` as the orthogonal vector to u

Explanation:

Given vectors a,b we can calculate the projection of a onto b by the formula

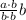`(a\cdot b)/(b\cdot b)b`. where
`\cdot` is the dot product of vectors.

For this example, we will take y = [1,3] and u = [6,2].

Let b be the projection of y onto u. That is

`b= (y\cdot u)/(u\cdot u)u = (1\cdot 6+ 3\cdot 2)/(6\cdot 6+2\cdot 2)(6,2) = (3)/(10)(6,2)`

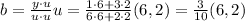
Now, we want to find an orthogonal vector w such that b+w = y. From this equation, we can find w by taking w = y-b. Then

`w = (1,3)-(3)/(10)(6,2) = (4)/(5)(-1,3)`

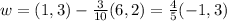
We must check that w and u are orthogonal. Note that if the vectors a,b are orthogonal, then the vectors a, kb are also orthogonal for every non-zero value of k. So, to check that a,kb are orthogonal, it suffices to check that a,b are orthogonal. We know that two vectors are orthogonal if and only if their dot product is zero. In our case, take the vector (6,2) and (-1,3). Note that

`(6,2)\cdot(-1,3) = -6+2\cdot3 = 0`

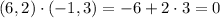
So, by the previous analysis, w and u are orthogonal.