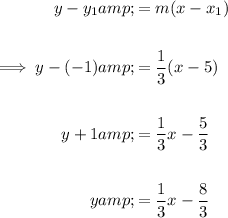Question

Consider the line - 3x +9y = 5.

Find the equation of the line that is perpendicular to this line and passes through the point (5, -1).
Find the equation of the line that is parallel to this line and passes through the point (5, -1).

Answer 1

• -3x+9y=5
• 9y=3x+5
• y=1/3x+5/9

Slope =m=1/3

Note that perpendicular lines have slopes negative reciprocal to each other .

• Slope of the perpendicular line=-3

Equation in point slope form

• y+1=-3(x-5)
• y+1=-3x+15
• y=-3x+14

And

parallel lines have equal slope

Equation of parallel line

• y+1=1/3(x-5)
• 3y+3=x-5
• 3y=x-8
• y=x/3-8/3

Answer 2

`\textsf{Perpendicular to given line}:y=-3x+14`

`\textsf{Parallel to given line}: y=\frac13x-\frac83`

Explanation:

Rewrite the given equation to make y the subject:

`\begin{aligned}-3x+9y &=5 \\ \implies 9y &=3x+5 \\ \implies y &=\frac13x+\frac59\end{aligned}`

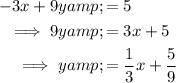
Therefore, the slope of the given equation is
`\frac13`.

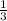If two lines are perpendicular to each other, the product of their slopes will be -1. Therefore, the slope (m) of the line that is perpendicular to the given line is:

`\begin{aligned}m * \frac13 & =-1\\ \implies m & =-3\end{aligned}`

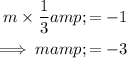
To find the equation of the line, substitute the found slope (-3) and the point (5, -1) into the point-slope form of a linear equation:

`\begin{aligned}y-y_1 & =m(x-x_1)\\ \implies y-(-1) &=-3(x-5) \\ y+1 & =-3x+15 \\ y &=-3x+14\end{aligned}`

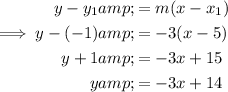
If two lines are parallel to each other, their slopes will be the same. Therefore, the slope (m) of the line that is parallel to the given line is
`\frac13`

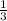
To find the equation of the line, substitute the slope (
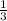`\frac13`) and the point (5, -1) into the point-slope form of a linear equation:

`\begin{aligned}y-y_1 & =m(x-x_1)\\\\ \implies y-(-1) &=\frac13(x-5) \\\\ y+1 & =\frac13x-\frac53 \\\\ y &=\frac13x-\frac83\end{aligned}`