Question

In the following shape, two semicircles have been placed at the end of a rectangle whose length is twice its height. Which of the following gives the length around this figure in terms of the semicircle's radius, r?

Answer 1

Perimeter of the figure is 2r(
`\pi` + 6)

Explanation:

Perimeter of a shape is total length of the boundaries of the shape. In the given question, we have two semicircles and a rectangle.

The circumference of a circle = 2
`\pi`r, thus the length of the arc of a semicircle =
`\pi`r.

The height of the rectangle is h, radius 'r' of the semicircle =
`(h)/(2)`

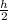
⇒ h = 2r

The perimeter of a rectangle = 2(l +b).

Given that: the length is twice its height, so that:

length = 2h

Perimeter of the rectangle = 2 (2h + h)

= 6h

But, h = 2r

Perimeter of the rectangle = 6 × 2r

= 12r

Perimeter of the figure in terms of the semicircle's radius =
`\pi`r + 12r +
`\pi`r

= 2
`\pi`r + 12r

= 2r(
`\pi` + 6)