Question

the center of a circe is located at (1,3). The point (0,1) lies on the circle. Find the equation of the circle

Answer 1

`(x-1)^(2)+(y-3)^(2) = 5`

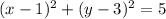
Explanation:

Given the general equation of a circle represented as:

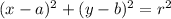`(x-a)^(2)+(y-b)^(2) = r^(2)` where:

(a, b) is the centre of the circle and r is the radius

Given the centre located a (1,3), to get the radius we will take the distance between the centre point of the circle the the point that lies on its circumference i.e (0,1).

Using the formula for calculating thee distance between 2 points, we have:

`r = \sqrt{ (x2-x1)^(2)+(y2-y1)^(2)}`

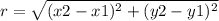
x1 = 1, y1 = 3, x2 = 0, y2 = 1

`r = \sqrt{ (0-1)^(2)+(1-3)^(2)}\\r=\sqrt{1^(2) +(-2)^(2)}\\r=√(1+4)\\r=√(5)`

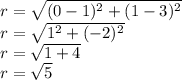
Substituting this values of the centre and radius of the circle into the general equation of a circle we have:

`(x-1)^(2)+(y-3)^(2) = (√(5)) ^(2)\\(x-1)^(2)+(y-3)^(2) = 5`

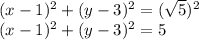
This gives the required equation of the circle.