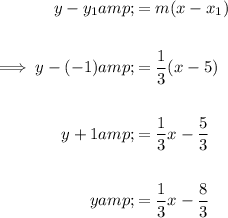Answer:


Explanation:
Rewrite the given equation to make y the subject:

Therefore, the slope of the given equation is
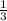 .
.
If two lines are perpendicular to each other, the product of their slopes will be -1. Therefore, the slope (m) of the line that is perpendicular to the given line is:
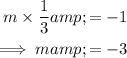
To find the equation of the line, substitute the found slope (-3) and the point (5, -1) into the point-slope form of a linear equation:

If two lines are parallel to each other, their slopes will be the same. Therefore, the slope (m) of the line that is parallel to the given line is
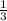
To find the equation of the line, substitute the slope (
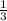 ) and the point (5, -1) into the point-slope form of a linear equation:
) and the point (5, -1) into the point-slope form of a linear equation: