Question

What is the total area of the figure? (square inches)

Answer 1

The area of the full figure is 60 square inches.

Explanation:

There are 4 triangles and one square in this figure. We can start by figuring out the area of the middle square, which would be
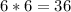`6*6=36` because we know the sides are all 6 inches.

Next, we can look at the triangles and see that their hypotenuses (the longest sides) are all the same length, that being 5 inches. This means that we only need to find the length of the third side and then multiply the area of one triangle by 4 to get the area of all the triangles.

The pythagorean theorem states that in any right triangle,
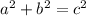`a^2 +b^2=c^2`, with
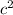`c^2` being the length of the hypotenuse. Since we know the length of the hypotenuse is 5 and one of the legs of the triangle is 4, we can insert this into the equation:
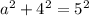`a^2+4^2=5^2`, which when simplified all the way gives us that
`a=3`.

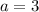Since a right triangle is half of a rectangle, the easiest way to find the area of the triangle is to multiply the measures of the two legs together and then divide by two:
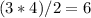`(3*4)/2=6`. Therefore, we know that each triangle in the picture has an area of 6.

Finally, you need to add all of the areas together to find the area of the full figure:
`36+6+6+6+6=60 in^2`

The area of the full figure is 60 square inches.

Hope this helps! :)

Answer 2

60

Explanation:

TOTAL SURFACE AREA = AREA OF SQUARE+2×(AREA OF TRIANGLE)

=(6×6)+2×(1/2×6×4)

=36+24=60 square inches

I hope it helped you