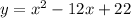Question

Write the quadratic function the points are (-1,35) (0,22) (1,11) (2,2) and (3,-5)

Answer 1

Explanation:

We only need 3 of those points and the standard form of the quadratic to find the function. The standard form is

`y=ax^2+bx+c`

From each coordinate we will sub in the x and y values. I am going to use the following 3 points from the table. (0, 22), (1, 11) and (2, 2). Always start with a coordinate that has an x value of 0 if you can! Filling in the standard form with the first of those 3 coordinates:

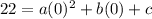`22=a(0)^2+b(0)+c` simplifies down to the fact that c = 22. That's good to know; now we have a value for one of the variables to fill into the next substitution:

`11=a(1)^2+b(1)+22`

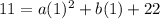
which simplifies down to

a + b = -11

Now for the 3rd and last coordinate:

`2=a(2)^2+b(2)+22`

which simplifies down to

4a + 2b = -20

Put the 2 bold equations together as a system and solve for one variable or the other. I chose to solve for b first, so in order to do that, I multiplied the first equation by a -4, giving me a new system:

-4a - 4b = 44

4a + 2b = -20

and

-2b = 24 so

b = -12. Now plug that back in and solve for a:

a - 12 = -11 so

a = 1.

Now we have the function:

`y=x^2-12x+22`