Question

PLEASE HELP ASAP

What are the explicit equation and domain for a geometric sequence with a first term of 3 and a second term of −9?

an = 3(−12)n − 1; all integers where n ≥ 1
an = 3(−12)n − 1; all integers where n ≥ 0
an = 3(−3)n − 1; all integers where n ≥ 1
an = 3(−3)n − 1; all integers where n ≥ 0

Answer 1

`a_1 = 3 , a_2 = -9`

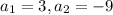
So then we have this:

`3 = a r^(1-1)= a`

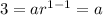
And using the second term we have:

`-9 = 3 r^(2-1)`

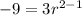
And solving for the value of r we got:

`r = (-9)/(3)= -3`

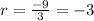
So then our general expression for this geometric sequence would be:

`a = 3 (-3)^(n-1) , n\geq 1`

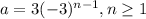
And the best answer would be:

an = 3(−3)n − 1; all integers where n ≥ 1

Explanation:

For this case we need to remember that the general formula for a geometric sequence is given by:

`a_n = a r^(n-1)`

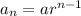
And for this case we have the following values for the sequence given:

`a_1 = 3 , a_2 = -9`

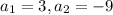
So then we have this:

`3 = a r^(1-1)= a`

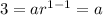
And using the second term we have:

`-9 = 3 r^(2-1)`

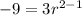
And solving for the value of r we got:

`r = (-9)/(3)= -3`

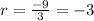
So then our general expression for this geometric sequence would be:

`a = 3 (-3)^(n-1) , n\geq 1`

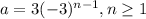
And the best answer would be:

an = 3(−3)n − 1; all integers where n ≥ 1