Question

\The lengths of a lawn mower part are approximately normally distributed with a given mean Mu = 4 in. and standard deviation Sigma = 0.2 in. What percentage of the parts will have lengths between 3.8 in. and 4.2 in.?

Answer 1

68.26% of the parts will have lengths between 3.8 in. and 4.2 in.

Explanation:

The lengths of a lawn mower part are approximately normally distributed

`\mu = 4`

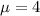
Standard deviation =
`\sigma =0.2`

We are supposed to find What percentage of the parts will have lengths between 3.8 in. and 4.2 in . i.e. P(3.8<x<4.2)

Formula :
`Z=(x-\mu)/(\sigma)`

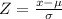
At x = 3.8

`Z=(3.8-4)/(0.2)`

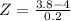
Z=-1

Refer the z table for p value

p value =0.1587

At x =4.2

`Z=(4.2-4)/(0.2)`

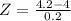
Z=1

Refer the z table for p value

p value =0.8413

P(3.8<x<4.2)=P(x<4.2)-P(x<3.8)=0.8413-0.1587=0.6826

So, 68.26% of the parts will have lengths between 3.8 in. and 4.2 in.