Question

An astronaut goes out for a "space-walk" at a distance above the earth equal to twice the radius of the earth. What is her acceleration due to gravity?

Answer 1

Acceleration due to gravity will be
`a=2.45 m/s^(2)`.

Step-by-step explanation:

We can use the gravitational force equation:

`F_(g)=G(mM_(e))/(R^(2))`

The F is equal to the weight of the astronaut, so we will have:

`ma=G(mM_(e))/(R^(2))`

`a=G(M_(e))/(R^(2))`

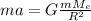
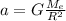
• M(e) is the mass of the earth
  `M_(e)=5.972*10^(24)kg`
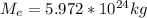
• R is the radius of the earth
  `R=6.377*10^(6)m`
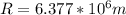
• G is the gravitational constant
  `G=6.67*10^(-11)m^(3)kg^(-1)s^(-2)`

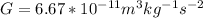
But the distance between the astronaut and the center of the earth is 2R, then we have:

`a=6.67*10^(-11)(5.972*10^(24))/((2*6.377*10^(6))^(2))`

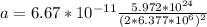
Therefore the acceleration due to gravity will be
`a=2.45 m/s^(2)`.

I hope it helps you!