Answer:
95% confidence interval for the proportion of all US buyers who would have chosen Opinion A is [0.28 , 0.32].
Explanation:
We are given that Two opposing opinions were shown to a random sample of 1,744 US buyers of a particular political news app.
The outcomes were as follows: 30% chose Opinion A, 64% chose Opinion B, and 6% chose "Neutral."
Firstly, the Pivotal quantity for 95% confidence interval for the population proportion is given by;
P.Q. =
 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of US buyers who chose Opinion A = 0.30
= sample proportion of US buyers who chose Opinion A = 0.30
n = sample of US buyers = 1,744
p = population proportion
Here for constructing 95% confidence interval we have used One-sample z test for proportions.
(a) SO, 95% confidence interval for the population proportion, p is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
 < 1.96) = 0.95
< 1.96) = 0.95
P(
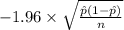 <
<
 <
<
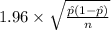 ) = 0.95
) = 0.95
P(
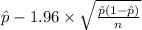 < p <
< p <
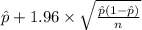 ) = 0.95
) = 0.95
95% confidence interval for p = [
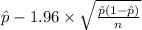 ,
,
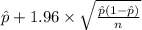 ]
]
= [
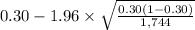 ,
,
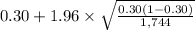 ]
]
= [0.28 , 0.32]
Therefore, 95% confidence interval for the proportion of all US buyers who would have chosen Opinion A is [0.28 , 0.32].
(b) The number of buyers that chose Opinion A and the number of buyers that did not choose Opinion A are both greater than 10, that is;
Number of buyers that did chose Opinion A =
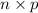
=
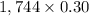 = 523.2
= 523.2
Number of buyers that did not chose Opinion A =
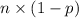
=
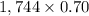 = 1220.8
= 1220.8
Now, this inference condition should have been met because if these were not met then we were not able to use the normal distribution statistics above because binomial distribution can be converted to normal distribution only when
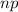 and
and
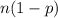 both are greater than 10.
both are greater than 10.