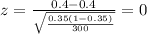Question

According to a Pew Research Center study, in May 2011, 35% of all American Points: 10 out of 10 adults had a smart phone (one which the user can use to read email and surf the Internet). A communications professor at a university believes this percentage is higher among community college students. She selects 300 community college students at random and finds that 120 of them have a smart phone. In testing the hypotheses:

H0: p = 0.4 versusHa: p > 0.4,what is the test statistic?z =________________. (Please round your answer to two decimal places.)

Answer 1

`z=\frac{0.4 -0.35}{\sqrt{(0.35(1-0.35))/(300)}}=1.82`

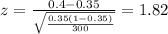
If we assume the hypothesis of:

H0: p = 0.4 versus Ha: p > 0.4

The statistic for this case would be:

`z=\frac{0.4 -0.4}{\sqrt{(0.35(1-0.35))/(300)}}=0`

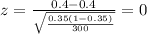
Explanation:

Information given

n=300 represent the random sample selected

X=120 represent the number of people that have smart phone

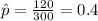`\hat p=(120)/(300)=0.4` estimated proportion of people with a smart phone

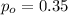`p_o=0.35` is the value that we want to test

z would represent the statistic

Hypothesis to test

For this case we want to test if the true proportion is hgiher than 0.35 since thats the claim given:

Null hypothesis:
`p\leq 0.35`

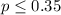
Alternative hypothesis:
`p > 0.35`

The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info we got:

`z=\frac{0.4 -0.35}{\sqrt{(0.35(1-0.35))/(300)}}=1.82`

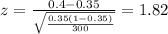
If we assume the hypothesis of:

H0: p = 0.4 versus Ha: p > 0.4

The statistic for this case would be:

`z=\frac{0.4 -0.4}{\sqrt{(0.35(1-0.35))/(300)}}=0`