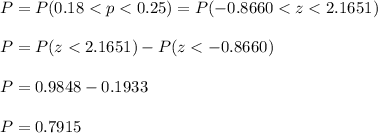Answer:
1. P(X≥35) = 0.0183
2. P(X≤21) = 0.0183
3. P(0.18<p<0.25) = 0.7915
Explanation:
We have the proportion for women: pw=0.22, and the proportion for men: pm=0.19.
1. We have a sample of 140 woman and we have to calculate the probability of getting 35 or more who do volunteer work.
This is equivalent to a proportion of
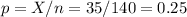
The standard error of the proportion is:
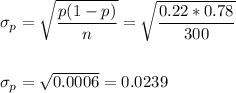
We calculate the z-score as:
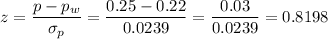
Then, the probability of having 35 women or more who do volunteer work in this sample of 140 women is:
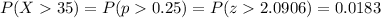
2. We have to calculate the probability of having 21 or fewer women in the group who do volunteer work.
The proportion is now:
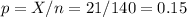
We can calculate then the z-score as:
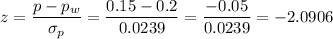
Then, the probability of having 21 women or less who do volunteer work in this sample of 140 women is:
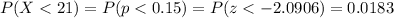
3. For the sample with men and women, we use the proportion for both, which is π=0.2.
The sample size is n=300.
Then, the standard error of the proportion is:
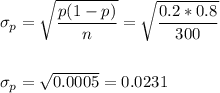
We can calculate the z-scores for p1=0.18 and p2=0.25:
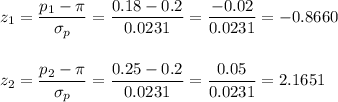
We can now calculate the probabilty of having a proportion within 0.18 and 0.25 as: