Answer:
using
 : 65.45 in³ (nearest hundredth)
: 65.45 in³ (nearest hundredth)
using
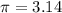 : 65.42 in³ (nearest hundredth)
: 65.42 in³ (nearest hundredth)
Explanation:
The radius of the sphere is half the side length of the cube (see attached diagram). Therefore, the side length of the cube = 2r
Given:
- volume of the cube = 125 in³
- side length of cube = 2r

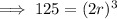
![\implies \sqrt[3]{125}=2r](https://img.qammunity.org/2023/formulas/mathematics/college/4hsxxtncrgj0402lo72nuv68677a4vhe1f.png)
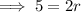
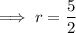
Substitute the found value of r into the volume of a sphere equation:
