Question

Laplace inverse (3s+4)/(s^2+
4s+29)​

Answer 1

Complete the square in the denominator to reveal a sum of squares:

`s^2+4s+29=(s+2)^2+25=(s+2)^2+5^2`

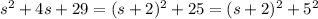
Recall the Laplace transforms of sine and cosine,

`L(\sin(at))=\frac a{s^2+a^2}`

`L(\cos(at))=\frac s{s^2+a^2}`

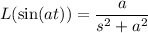
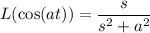
as well as the frequency shift property,

`L(e^(at)f(t))=F(s-a)`

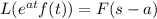
where
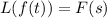`L(f(t))=F(s)` is the Laplace transform of
`f(t)`.

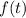Rewrite the given transform as

`(3s+4)/(s^2+4s+29)=(3(s+2))/((s+2)^2+5^2)-\frac25\frac5{(s+2)^2+5^2}`

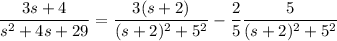
The inverse transforms then follows:

`F(s+2)=(3(s+2))/((s+2)^2+5^2)\implies f(t)=3e^(-2t)L^(-1)\left(\frac s{s^2+5^2}\right)`

`\implies f(t)=3e^(-2t)\cos(5t)`

`F(s+2)=-\frac25\frac5{(s+2)^2+5^2}\implies f(t)=-\frac25e^(-2t)L^(-1)\left(\frac5{(s+2)^2+5^2}\right)`

`\implies f(t)=-\frac25e^(-2t)\sin(5t)`

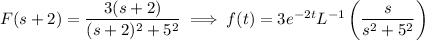
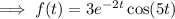
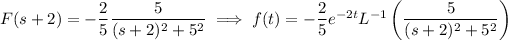
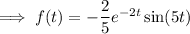
So we end up with (after some regrouping)

`L^(-1)\left((3s+4)/(s^2+4s+29)\right)=\boxed{\frac{e^(-2t)}5(15\cos(5t)-2\sin(5t))}`