Question

A wire carries a 11.3-mA current along the +x-axis through a magnetic field = (16.2 + 2.4 ĵ) T. If the wire experiences a force of -15.7 N as a result, how long is the wire?

Answer 1

The length of the wire is 579 m

Step-by-step explanation:

Given;

current on the wire, I = 11.3-mA

magnetic field of the wire, B = (16.2i + 2.4 ĵ) T

Magnitude of force experience by the wire, F = 15.7 N

Magnitude of force experience by current carrying wire at a given a magnetic field strength is calculated as;

F = BILsinθ

Where;

B is magnitude of magnetic field

F is the force on the wire

L is length of the wire

θ is direction of the magnetic field

`B = √(16.2^2 +2.4^2) = √(268.2) = 16.377 \ T`

`tan \theta = (2.4)/(16.2) \\\\tan \theta = 0.1482\\\\\theta = tan^(-1)(0.1482) \\\\\theta = 8.43^o`

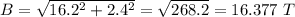
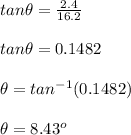
Length of the wire is calculated as;

`L = (F)/(BIsin \theta) = (15.7)/(16.377*11.3*10^(-3)*sin(8.43)) = 578.9 \ m`

Therefore, the length of the wire is 579 m