Answer:
17. A
18. B
Explanation:
17. We need to find the longest side length. Remember that in a triangle, the smallest angle corresponds to the shortest side length and the largest angle corresponds to the longest side length.
Here, we already know two angles are 75 and 60, which means that the third angle is 180 - 75 - 60 = 45 (because all angles of a triangle add up to 180). Since 45 is the smallest angle, it corresponds to the shortest side, which we know is 10 units. Since 75 is the largest angle, it corresponds to the longest side, which we want to find.
We now use the Law of Sines, which states that for a triangle with side lengths a, b, and c and angles A, B, and C:
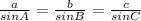
Here, let's say that a = 10, A = 45, and B = 75. Then:
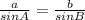
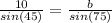
Remember that sin(45) = √2/2 and sin(75) = (√2 + √6) / 4. Plug these in and solve for b, which is the longest side we want to find:
b = [(√2 + √6) / 4] * [10 / (√2/2)] = 5 + 5√3 = 5(1 + √3)
The answer is thus A.
18. We need to use trigonometry for this. Notice that in triangle ABC, we can write the tangent (which is opposite divided by adjacent) expression:
tan(30) = BC / AB = h / (4 + x)
Remember that tan(30) = √3/3. So:
h/(4 + x) = √3/3
Now we can also write a tangent expression for triangle BDC:
tan(60) = BC / DB = h/x
Remember that tan(60) = √3, so:
h/x = √3
We're looking for x, so write h in terms of x from the second equation:
h/x = √3
h = x√3
Plug this in for h in the first equation:
h/(4 + x) = √3/3
(x√3) / (4 + x) = √3/3
x√3 = (4√3 / 3) + x√3/3
x√3 - x√3/3 = 4√3/3
2x√3/3 = 4√3/3
x = 2
The answer is thus B.